• 前章での「部分型付けのある単純型付きラムダ計算」の定義は、構文主導ではない
• 構文主導とは、構文に基づいて、動作や意味が決まること
• ボトムアップでは型検査アルゴリズムは得られない

★ 何が問題点か

• 主な問題は、包摂規則(T-SUB)と推移律(S-TRANS)
• 単一のメタ変数 t を使って定義されているため、ほぼ任意の式に対して規則が適用可能になってしまう
  => どの規則を試すべきかが自明ではなく、アルゴリズムとしては不十分
• さらに、S-TRANSには結論部に束縛されないメタ変数 U が前提部に出現する
  => 推測できる U の数は無限個あるため、このまま実装するには不適切

Γ├ t : S S <: T T-SUB Γ├ t : T

S <: U U <: T S-TRANS S <: T

これらの問題は既存の規則を、構文主導的な推論規則の集合からなる以下の２つの関係で置き換えれば、解決できる。

1. アルゴリズム的部分型関係
2. アルゴリズム的型付け関係

また、書き換え前後の表現が一致することを証明することにより、この書き換えの正しさを示す。

例えば、t1 が T→U 型をもち、t2 が S 型を持つとして、関数適用 t1 t2 に出会ったとき、「SはTの部分型か」を判断するために、部分型検査器アルゴリズムが呼び出される。

アルゴリズム的関係には、規則S-TRANS, S-REFLがない。
S-TRANSをなくすには、まず深さ・幅・並び替えの部分型付けを一つにまとめる規則を追加する必要がある。

{ li | i∈1..n } ⊆ { kj | j∈1..m }	kj = li ならば、Sj <: Ti	S-RCD
{ kj : Sj | j∈1..m } <: { li : Ti | i∈1..n }

> つまり..
レコードA{ kj : Sj }、レコードB{ li : Ti } について

• レコードAのラベル名の集合が、レコードBのラベル名の集合を含んでる
• それぞれの同じラベル名 kj, li について Sj <: Ti

ならば、レコードAはレコードBの部分型。

このS-RCDが、S-RCD-DEPTH, S-RCD-WIDTH, S-RCD-PERM（部分型付け規則の一部）を置き換えるものとして十分だということを、次の補題で証明してみよう。。

補題 16.1.1
S-RCD-DEPTH + S-RCD-WIDTH + S-RCD-PERM を含む部分型付け規則で S <: T を導出できる
⇄ S-RCD で S <: T を導出できる

各iに対して Si <: Ti	S-RCD-DEPTH
{ li : Si | i∈1..n } <: { li : Ti | i∈1..n }

	S-RCD-WIDTH
{ li : Ti | i∈1..n+k } <: { li : Ti | i∈1..n }

{ kj : Sj | j∈1..n } は { li : Ti | i∈1..n } の並び替えである	S-RCD-PERM
{ kj : Sj | j∈1..n } <: { li : Ti | i∈1..n }

⇅

{ li | i∈1..n } ⊆ { kj | j∈1..m }	kj = li ならば、Sj <: Ti	S-RCD
{ kj : Sj | j∈1..m } <: { li : Ti | i∈1..n }

証明）
導出に関する帰納法により、示す。

(→) S <: T を導出する最後の規則で場合わけをする

1. S-RCD-DEPTHの場合
   S-RCD において、{ li } ≡ { kj } であるようなケース。{ li } ≡ { kj } より、前提部 { li } ⊆ { kj } を導くことができる。
2. S-RCD-WIDTHの場合
   自明
3. S-RCD-PERMの場合
   { kj : Sj } が { li : Ti } の並び替えであるなら、前提部 { li } ⊆ { kj } を導くことができる。

(←) S <: T を導出する最後の規則が S-RCDであるとして、

• 【{ li | i∈1..n } ⊆ { kj | j∈1..m } 】の部分
  S-RCD-WIDTHに対応
• 【kj = li ならば、Sj <: Ti】の部分
  ラベルの対応づけを行ってから型の対応関係を求めているので、S-RCD-PERM と S-RCD-DEPTH に対応

の性質と、帰納法の仮定で示せれる。

この証明によって、S-RCDが、S-RCD-DEPTH, S-RCD-WIDTH, S-RCD-PERM を置き換えるものとして十分だということが示せた。
結果的に得られる型システムを、以下（図16-1) のようにまとめることができる。

図16-1: レコードのある部分型関係

S-REFL S <: S

S <: U U <: T S-TRANS S <: T

S-TOP S <: TOP

T1 <: S1 S2 <: T2 S-ARROW S1 → S2 <: T1 → T2

{ li | i∈1..n } ⊆ { kj | j∈1..m }	kj = li ならば、Sj <: Ti	S-RCD
{ kj : Sj | j∈1..m } <: { li : Ti | i∈1..n }

では、次にS-TRANS, S-REFLが別のアルゴリズム的関係に置き換えることができることを示そう。

補題 16.1.2
(1) すべての型Sについて、S <: S はS-REFLを使わずに導出できる
(2) もし S <: Tが導出可能ならば、 S <: T は S-TRANSを使わずに導出できる

証明）
(1) 型の大きさに関する帰納法で示す。

• S ≡ Top の場合
  Top <: Top は、S-TOPにより示せる
• S ≡ T1 → T2 の場合
  T1 → T2 <: T1 → T2 は、S-ARROW により T1 <: T1, T2 <: T2 が成り立てばよいが、
  これは帰納法の仮定により成立する。
• S ≡ { ki : Si ( i∈1..n ) } の場合
  補題16.1.1(→)より、S-RCD-DEPTHはS-RCDで代用することができる。
  これを適用すると、各iに対して Si <: Si が成り立てばよいことになるが、これは帰納法の仮定により成り立つ。
  

(2) 型の大きさに関する帰納法で示す。
S ≡ Top の場合

• T ≡ Top の場合
  S-TOPにより成立。
• T ≡ T1 → T2 の場合
  そもそも導出不可能。(Topの定義より)
• T ≡ { li : Si } の場合
  そもそも導出不可能。(Topの定義より)

S ≡ S1 → S2 の場合

• T ≡ Top の場合
  S-TOPにより成立。
• T ≡ T1 → T2 の場合
  S-ARROWにより、T1 <: S1, S2 <: T2 が成り立てばよい。あとは帰納法の仮定。
• T ≡ { li : Ti } の場合
  そもそも導出不可能。※1

S ≡ { kj : Sj } の場合

• T ≡ Top の場合
  S-TOPにより成立。
• T ≡ T1 → T2 の場合
  そもそも導出不可能。※1
• T ≡ { li : Ti } の場合
  S <: T は導出可能なので、補題15.3.2(2)'より、
  { li } ⊆ { kj } かつ li = kj では Sj <: Ti である。つまり、S-RCDを適用すればおk。

※1 補題15.3.2(2)を再証明することにより


よって、アルゴリズム的部分型付けは以下 (図16-2) のようにまとめることができる。
※ 本章では、前章で扱った部分型付け判断式 S <: T の代わりに、|→ S <: T (「Sはアルゴリズム的にTの部分型になる」)という別の関係として表記する。
図16-2: アルゴリズム的部分型付け

	SA-TOP
|→ S <: TOP

|→ T1 <: S1	|→ S2 <: T2	SA-ARROW
|→ S1 → S2 <: T1 → T2

{ li | i∈1..n } ⊆ { kj | j∈1..m }	kj = li ならば、|→ Sj <: Ti	SA-RCD
|→ { kj : Sj | j∈1..m } <: { li : Ti | i∈1..n }

演習 16.1.3
もし、型Boolを追加したら、これらの性質はどう変化するだろうか。

証明）
型Boolを追加すると、型の構文規則が以下のようになる。

T	::=	Top
		T → T
		{ li : Ti ( i∈1..n ) }
		<b>Bool</b>

ベースとなる型がひとつ増えるわけなので、以下のような規則を追加する必要がでてくる。

	SA-BOOL
|→ Bool <: Bool

定義 16.1.4
アルゴリズム的部分型関係は、図16-2の規則に閉じた最小の関係である。

• 健全性 アルゴリズム的規則で導出できるすべての部分型付け判断式は、宣言的規則でも導出できる
• 完全性 宣言的規則で導出できる全ての部分型付け判断式がアルゴリズム的規則でも導出できる

命題 16.1.5
[健全性と完全性] S <: T のとき、かつそのときのみ |→ S <: T

証明）
どちらも導出に関する帰納法で示す。
(→)
S <: T 導出木で、最後に適用した規則で場合分けする。

• S-REFL の場合
  先の補題と導出の大きさに関する帰納法の仮定より。
• S-TRANS の場合
  先の補題と導出の大きさに関する帰納法の仮定より。
• S-TOP の場合
  SA-TOPを適用すればよい。
• S-ARROW の場合
  導出の大きさに関する帰納法の仮定より、|→ T1 <: S1, |→ S2 <: T2 が成り立つので、これに SA-ARROWを適用すればよい。
• S-RCD の場合
  略

(←)
略


これで、アルゴリズム的部分型関係を検査するアルゴリズムが完成した＾＾
このアルゴリズムを擬似コードとして書くと以下のようになる。

subtype(S, T)	=	if T = Top then true
		else if S = S1 → S2 and T = T1 → T2
		  then subtype(T1, S1) ^ subtype(S2, T2)
		else if S = { kj : Sj | j∈1..m } and T = { li : Ti | i∈1..n }
		  then { li | i∈1..m } ⊆ { kj | j∈1..m }
		    ^ すべてのiに対して、j∈1...mが存在し、kj = li かつ subtype(Sj, Ti)
		else false

最後に、この関係が全域的、つまり、この再帰関数subtypeが任意の入力に対して有限時間内に結果を返すことを検証する必要がある。

命題 16.1.6
[停止性] もし |→ S <: T が導出可能ならば、subtype(S, T)は true を返す。そうでないなら、false を返す。

証明）
再帰時の引数の大きさの和は、入力S, Tの大きさの和より真に小さいので、ちゃんと止まる。


【「はじめっから、アルゴリズム的定義でやれば良いのでは？」と思った人へ】
まあその通りなのだが、型付け関係の正当性を示すためには、「部分型付けが反射的・推移的である」ことを知る必要があるので、どっちの定義を先に持ってきても作業量はさほど変わらないよ。

部分型関係をアルゴリズム的にした今、型付け関係もアルゴリズム的にする必要がある。現在、T-SUBだけが構文主導でない型付け規則であるが、これをなくすことを考えてみよう。

Γ├ t : S	S <: T	T-SUB
Γ├ t : T

簡単にT-SUBを消すことはできない。T-SUBを使う目的は「関数によって期待される型と、引数の実際の型との隔たりを埋めること」である。下の例は、T-SUBが型付けにおいて重要な役割を果たす唯一の状況である。

(λr:{ x:Nat }. r.x) { x=0, y=0 }

他の全ての場合では、部分型付け判断式を別の導出によって証明することができる。T-SUBを木の根に向かって動かし「後回し」にする導出である。このテクニックをここで少し紹介する。

略

演習 16.2.1
この実験を仕上げるため、T-RCD または T-PROJ の前で規則T-SUBが使われているような導出において、どのように同様の再配置を実行すればよいかを示せ。

証明）
省略

さて、このことからT-SUBが必要となる場所はただ一つ、関数適用だけになった。この場合にT-SUBなしで対応するために、関数適用の規則を少し強力なもので置き換えてみよう。

Γ├ t1 : T11 → T12	Γ├ t2: T2	T2 <: T11
Γ├ t1 t2 : T12

↑前提部にT-SUBのインスタンスの一つ「T2 <: T11」を合体させた！これにより、全ての導出がT-SUBを使わない形になり、元の型システムと同じ項の集まりに型を割り当てる【構文主導的な型付け規則の集合】が得られた（＾ー＾）b

よって、アルゴリズム的型付けは以下 (図16-3) のようにまとめることができる。
※アルゴリズム的部分型付け規則と同様、宣言的関係と区別するため、Γ|→ t : T と書くことにする。
図16-3: アルゴリズム的型付け

x : T ∈ Γ TA-VAR Γ|→ x : T

Γ、x : T1 |→ t2 : T2 TA-ABS Γ|→ λx:T1. t2 : T1 → T2

Γ|→ t1 : T1	Γ|→ t2: T2	T1 = T11 → T12	|→ T2 <: T11	TA-APP
Γ|→ t1 t2 : T12

各iに対して、Γ|→ ti : Ti	TA-RCD
Γ|→ { l1=t1 ... ln=tn } : { l1 : T1 ... ln : Tn }

t1 : R1	R1 = { l1 : T1 ... ln : Tn }	TA-PROJ
Γ|→ t1.li : Ti

定義 16.2.2
アルゴリズム的型付け関係は図16-3の規則について閉じた最小の関係である。

演習 16.2.3
ある項にアルゴリズム的型付け規則で割り当てられる型が評価によって、減少しうることを示せ。これは、ある２つの項 s と t で、アルゴリズム的型付けで S と T に型付けされ、s →* t かつ T <: S だが、S !<: T となるようなものを見つけることで示せ。

証明）

• しらん

部分型付けのときと同様に、アルゴリズム的型付け関係が、元の宣言的な規則について、健全かつ完全であることを証明していく。

定理 16.2.4
[健全性] Γ|→ t : T ならば Γ├ t : T となる。
アルゴリズム的型付け導出に関する単純な帰納法により、示せ。

証明）
省略


定理 16.2.5
[完全性、最小型付け] もし Γ├ t : T ならば、ある S <: T が存在して、Γ|→ t : S

証明）
宣言的な型付け導出に関する帰納法により証明。

• T-VAR の場合 t = x
  このとき、Γ(x) = T これに TA-VARを適用すれば、Γ|→ x : T
  
  
• T-ABS の場合 t = λx:T1. t2
  このとき、Γ, x : T1├ t2 : T2 かつ T = T1 → T2
  帰納法の仮定より、ある S2 <: T2 に対し、Γ, x : T1├ t2 : S2
  これにTA-ABSを適用すると、Γ├t : T1 → S2
  S-ARROWより、T1 → S2 <: T1 → T2
  
  
• T-APP の場合 t = t1 t2
  このとき、Γ├t1 : T11 → T12 かつ Γ├t2 : T11 かつ T = T12
  帰納法の仮定より、ある S1 <: T11 → T12 に対し、Γ |→ t1 : S1 であり、ある S2 <: T11 に対し、Γ├t2 : S2 である。
  補題15.3.2より、S1 は T11 <: S11 かつ S12 <: T12 なる S11 と S12 に対して S11 →S12 という形をもつ。
  S-TRANSより、S2 <: S11。アルゴリズム的部分型付けの完全性より、|→ S2 <: S11
  さらに TA-APP より、Γ├t1 t2 : S12
  
  
• T-RCD の場合 t = { li=ti }
  このとき、各iに対し Γ├ti : Ti かつ T = { li:Ti }。あとは帰納法の仮定とTA-RCDより。
  
  
• T-APROJ の場合 t = t1.lj
  このとき、Γ├ t1 : { li:Ti } かつ T = Tj。あとは略
  
  
• T-SUB の場合 前提条件より、t : S' かつ S' <: T
  帰納法の仮定より、ある S <: S' が存在して、Γ├ t : S であるが、このときS-TRANSより、S <: T。

定理 16.2.6
もし部分型付け規則 S-ARROW をなくし、それ以外の宣言的な部分型付け規則、および型付け規則はそのままにした場合、この体型は最小型付けの性質を持つか。もしそうならば、それを証明せよ。そうでないなら、最小型を持たない、型付け可能な項の例を示せ。

証明）
項 λx: {a : Nat}. x は宣言的な規則の下では、

• {a:Nat} → {a:Nat}
• {a:Nat} → Top

のどちらの型ももつ。

しかし、S-ARROWをなくすと、これらの型は互いの部分型にならない。
つまり、下式を証明できなくなる。

{a:Nat} → {a:Nat} <: {a:Nat} → Top

分岐があると、部分型の扱いが少しややこしくなる。なぜなら、どの場合に分岐しても必ず部分的に同じ型でなくてはいけなくなるから。
例えば、以下のような導出規則T-IFがあるとする。

Γ├ t1 : Bool	Γ├ t2 : T	Γ├ t3 : T	T-IF
Γ├ if t1 then t2 else t3 : T

このとき、if true then { x=true, y=false} else { x=false, z=true } は { x: Bool } という型をもつ。
なぜなら、

• then節は最小型 { x: Bool, y: Bool } を持ち、これはT-SUBによって { x: Bool } に昇格できる
• else節の型 { x: Bool, z: Bool } も { x: Bool } に昇格できる
• よって、{ x: Bool, y: Bool } と { x: Bool, z: Bool } の両方の上位型である任意の型をもつ
• この中で最小の型は { x: Bool }　である

ためである。

この型は分岐の型についての結びとしばしば呼ばれる。これは半順序における２つの要素の結びに相当するからである。

定義 16.3.1

• [結び] 型の二つ組S, Tに対して、ある型 J が S と T の結びであるとは、S <: J かつ T <: J かつ 任意の型 U に対して、S <: U かつ T <: U ならば J <: U となること。
• [交わり] 型の二つ組S, Tに対して、ある型 M が S と T の交わりであるとは、M <: S かつ M <: T かつ、任意の型 L に対して、L <: S かつ L <: T ならば、L <: M となること。
• [下に有界] 型の二つ組S, Tについて、ある型 L が存在して、L <: S かつ L <: T となるとき、下に有界であるという。
• [有界な交わり] 下に有界である全ての S と T について、S と T の交わり M が存在するような部分型関係は、有界な交わりを持つという。

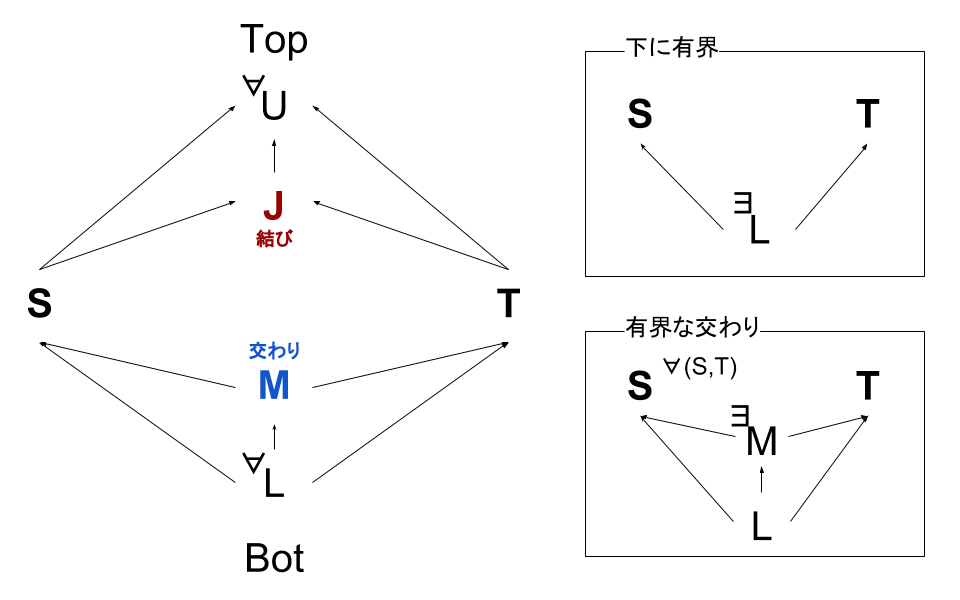
注釈

• 結びの関係を、S v T = J と表記する。
• 交わりの関係を、S ^ T = M と表記する。

この節で考える部分型関係は結び (最大でTop) を持つが交わりを持たない。
例えば、型 {} と Top → Top は共通の部分型を全く持たないため、最大の共通の部分型は存在しない。

結びや交わりは唯一である必要はない。
例えば、{ x : Top, y : Top, z : Top } と { x : Top, y : Top, w : Top } は、結びとして、{ x : Top, y : Top } と { y : Top, x : Top } を持つ。

同じ型の二つ組に対する、二つの異なる結び J1, J2（または交わり）は必ず、お互いの部分型になる。

命題 16.3.2
(1) すべての型の二つ組S, Tについて、ある型Jが存在して、S v T = J
(2) 共通の部分型を持つ、すべての型の二つ組S, Tについて、ある型Mが存在して、S ^ T = M

証明）
どちらの場合も、それを求めるアルゴリズムを示せればよい。

S v T =	Bool	S = T = Bool の場合
	M1 → M2	S = S1 → S2,
		T = T1 → T2,
		S1 ^ T1 = M1,
		S2 v T2 = J2 の場合
	{ jl:Jl | l∈1..q }	S = { kj:Sj | j∈1..m }
		T = { li:Ti | i∈1..n }
		{ jl | l∈1..q } = { kj | j∈1..m } ∩ { li | i∈1..n }
		各 jl = kj = li に対して Sj v Ti = Jl の場合
	Top	それ以外

S ^ T =

省略

演習 16.3.3
if true then false else {} の最小型は何か。これは我々の求めているものか。

証明）

• then節は最小型として Bool を持つ
• else節は最小型として {} を持つ
• 両節の上位型の中で最小の型はTop
• よって、全体として Top 型になる

任意の型Sに対して S <: TOP が成り立つ(SA-TOP)ので、あまり情報として意味がない。


演習 16.3.4
結びと交わりを計算するアルゴリズムを、15.5節で記述されたような参照を持つ手続き型言語へ拡張することは簡単か。非変なRefを共変なSourceと反変なSinkに詳細化した15.5節での参照の扱いについてはどうか。

S1 <: T1	S-SOURCE
Source S1 <: Source T1

T1 <: S1	S-SINK
Sink S1 <: Sink T1

証明）
Ref の追加に関しては、アルゴリズムを拡張するだけでよい(省略)。
しかし、Source, Sink 構築子に詳細化すると、部分型関係が結び・交わりを持たなくなる問題が発生する。
例えば、

• Ref { a:Nat b:Bool } <: Source { a: Nat }
• Ref { a:Nat } <: Sink { a:Nat b:Bool }

であるが、これらは共通の下界を持たない。(Refは非変であるため)
この問題を回避するためにはSource, Sinkを両方でなく、どちらか一方だけを導入すること。これらの具体的な実装については、後の章でやる予定。

もし部分型関係に最小型Bot(15.4節)を加える場合、拡張が必要。
まず、アルゴリズム的部分関係に一つの公理を追加する。

	SA-BOT
|→ Bot <: T

次に、アルゴリズム的型付け関係には、二つの規則を追加する。

Γ|→ t1 : T1	T1 = Bot	Γ|→ t2 : T2	TA-APPBOT
Γ|→ t1 t2 : Bot

Γ|→ t1 : R1	R1 = Bot	TA-PROJBOT
Γ|→ t1.li : Bot

Botは任意の他の型を持つことができる。

Bot型のものには無条件に任意の型の引数を関数適用できる。
これはT-SUBを使って、Botをどんな関数型にもできるため。射影(TA-PROJBOT)に関しても同様。

演習 16.4.1
この言語が条件式も持っていたとする。このとき、ifについてのアルゴリズム的型付け規則を追加する必要はあるか。

証明）
追加の必要あり。

Γ|→ t1 : T1	T1 = Bot	Γ|→ t2 : T2	Γ|→ t3 : T3	T2 v T3 = T	TA-IF
Γ|→ if t1 then t2 else t3 : T

など。
Bot は空なため（実際にBot型となるような項は存在しない）、t1 の評価は結果を返すことはない。


28.8節で、Botが有界量化と合わさったときにより複雑になるが、今節でのBotの追加は容易い。