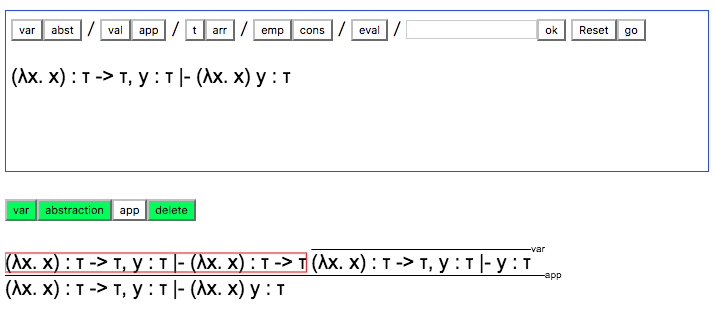
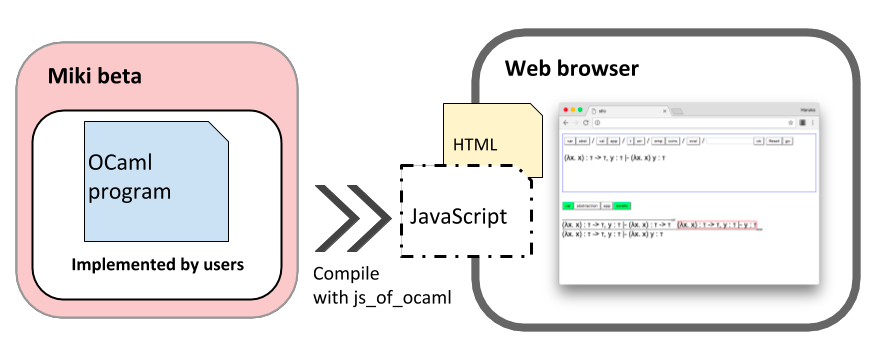
Miki Beta is based on datatype-generic programming
[1].
Datatype-generic programming provides the genericity over the stucture of types.
It realizes such a genericity by representation of datatypes with a sum-of-product structure.
Here we will learn PolyP
[2] as an example.
Two questions:
- Define tree and list structures.
- Implement a function `get_params` that returns a list of all values
the given term (tree or list typed) contains
First, let us see how they can be defined in the standard OCaml.
(* Standard definition of tree datatype in OCaml *)
| type tree_t = |
| | Leaf |
| | Node of tree_t * int * tree_t |
(* Standard definition of list datatype in OCaml *)
| type list_t = |
| | Empty |
| | Cons of int * list_t |
In the above program, tree and list structures are defined as OCaml standard datatypes.
Then, let's implement a `get_param` function for their types.
(* get_params_for_tree: tree_t -> int list *)
let rec get_params_for_tree t = match t with
| Leaf -> []
| Node (l, n, r) -> (get_params_for_tree l) @ [n] @ (get_params_for_tree r)
(* get_params_for_list: list_t -> int list *)
let rec get_params_for_list t = match t with
| Empty -> []
| Cons (n, r) -> n :: (get_params_for_list r)
Although the above two functions look similar to each other,
you have to define them separately.
It is because of the type dependency.
Whenever you define a new datatype, you have to add a corresponding function.
On the other hand, using datatype-generic terms,
the main functionality of `get_params` can be defined in a single function as follows.
(* Definition of the datatype to represent generic world *)
| type code_t = |
| | U | (* unit type | *) |
| | P | (* parameter type | *) |
| | I | (* recursive type | *) |
| | Plus of code_t * code_t | (* sum type | *) |
| | Times of code_t * code_t | (* product type | *) |
(* Definition of a represented tree datatype *)
let tree_type =
Plus (U, Times (Times (I, P), I))
(* Definition of a represented list datatype *)
let list_type =
Plus (U, Times (P, I))
(* get_params: code_t -> code_t -> type_f -> int list *)
let rec get_params c r t = match (c, t) with
| (U, Unit ()) -> []
| (I, Rec (t')) -> get_params r r t'
| (P, Par (n)) -> [n]
| (Plus (c1, c2), Sum (Left (t'))) -> get_params c1 r t'
| (Plus (c1, c2), Sum (Right (t'))) -> get_params c2 r t'
| (Times (c1, c2), Pair (t1', t2')) -> (get_params c1 r t1') @ (get_params c2 r t2')
| _ -> failwith "Should not happen"
(* get_params_for_tree: type_f -> int list *)
let get_params_for_tree = get_params tree_type tree_type
(* get_params_for_list: type_f -> int list *)
let get_params_for_list = get_params list_type list_type
Even if you add another representation of datatype, the above function `get_params` works for it.
This is how the datatype-generic programming makes your program smaller.
Miki Beta mixes features of PolyP and Indexed Functors
[3].
While the above example follows PolyP,
Indexed Functor represents indexed datatypes
so that it can construct mutually recursive datatypes.