Miki beta - User manual

We have the definition of `Simply Typed Lambda Calculus` below.

• Term

	var	:=	{ x, y, z, ... }
	const_typ	:=	{ α, β, τ ... }
0th term,	value	:=	var	(var)
		|	(λ var. exp)	(abst)
1st term,	exp	:=	value	(value)
		|	exp exp	(app)
2nd term,	typ	:=	const_typ	(const)
		|	typ → typ	(arrow)
3rd term,	env	:=	[]	(empty)
		|	exp : typ, env	(cons)
4th term,	judgement	:=	env ├ exp : typ	(eval)



• Axioms, inference rules

	Var
Γ, x : τ ├ x : τ

	Γ, x : τ1 ├ y : τ2	Abstraction
Γ ├ (λx : τ1. y) : τ1 → τ2

Γ ├ y : τ1 → τ2	Γ ├ x : τ1	App
Γ ├ y x : τ2

Let's define STLC terms. You should construct your terms by combining representation of types. We call the representation of type Code. Code is defined in Miki Beta as follows.

Code consists of five elements:

• U for unit types
• I i for recursion types to i-th term
• P for parameter types
PI means `integer type`, PS `string type` and PF `float type`
• Plus for meaning "or"
• Times for pair of two Code

Represent each type of terms by using Code. STLC terms can be represented as follows.

term-index	name	Representation of type
0th	value	Plus (PS, Times (PS, I 1))
1st	exp	Plus (I 0, Times (I 1, I 1))
2nd	typ	Plus (PS, Times (I 2, I 2))
3rd	env	Plus (U, Times (Times (I 1, I 2), I 3))
4th	judgement	Times (I 3, Times (I 1, I 2))

For simplicity, we refer to each term-index as `{term's name}_i` from here. `value_i` refers to the index 0, and `env_i` to 3 for example.

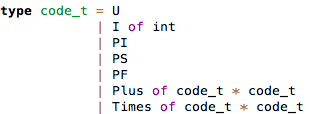
You should define each term in OCaml program, and give them to Miki Beta. Let me show how to define `value` term as an example.
`value` term consists of two alternatives: `var` and `abst`. For each alternative, you should define the three features:

1. constructor's name (string typed)
2. representation of the type (Code typed)
3. renderer function

We know that each three features for `var` and `abst` are as follows.

1.	constructor's name	:	"var"
2.	representation of the type	:	PS
3.	renderer function	:	x
			(when the string parameter for PS is `x`)
1.	constructor's name	:	"abst"
2.	representation of the type	:	Times (PS, I expr_i)
3.	renderer function	:	λx. y
			(when the string parameter for PS is `x` and `I expr_i` is rendered as `y`)

As OCaml program, you should define the three features as a tuple. Then collect them in a single list.

let value_def =
[("var",
  PS,
  fun t -> t 0);
 ("abst",
  Times (PS, I expr_i),
  fun t -> combineH [create_str "(λ"; t 0; create_str ". "; t 1; create_str ")"])
]

After defining the list of tuples for each term (say `value_def`, ... , `judgement_def`), then store all of them in one list named `termDefs`. They should be paired with string representation of meta variable (how you want to draw meta variable for the termX). Note that each of list indexes corresponds to a term's ordinal number. You define a module, which contains the list `termDefs` and an int `top_i`. `top_i` is the ordinal number for the outermost term. Both `termDefs` and `top_i` must be declared with these names.

module Terms = struct
  (* top_i : int *)
  (* The ordinal number for the outermost term *)
  let top_i = judgement_i

  (* termDefs : string * termdef_t list *)
  (* list of definitions of each terms' name, types, and how to draw them *)
  let termDefs = [("v", value_def); ("e", exp_def); ("t", typ_def); ("env", env_def); ("judgement", judgement_def)]
end

Pass the defined module to a functor in Miki Beta `Fix.F`, and you will finally get the wrapped module that is needed to create the GUI world. Let us call the module `Fixs`.

module Fixs = Fix.F (Terms)

Lastly, we would like to define axioms and inference rules in STLC. We should use the module `Fixs` here. The module `Fixs` enables two operation for x-th term:

• Make a mata variable by `Fixs.make_meta {x}`
• Construct a new specific term (not a meta variable) by `Fixs.make {x} {name} {plist} {rlist}`
where
• `name` is constructor's name to specify an alternative (e.g. "var", "abst")
• `plist` is a list of parameter types `PI`, `PS`, or `PF`, which a new term contains them in in-order traversal
• `rlist` is a list of terms for recursion types, which a new term contains them in in-order traversal.

With these two interfaces, you can define your rules.

(* Functions to construct each term *)
let var s = Fixs.make value_i "var" [s] []
let abst ps e = Fixs.make value_i "abst" [ps] [e]
let var s = Fixs.make value_i "var" [s] []
let valu v = Fixs.make expr_i "val" [] [v]
let arrow t1 t2 = Fixs.make type_i "arr" [] [t1; t2]
let app e1 e2 = Fixs.make expr_i "app" [] [e1; e2]
let judgement e ve t = Fixs.make eval_i "eval" [] [e; ve; t]

(* `var` axiom *)
let rule_vars () =
  let e = Fixs.make_meta expr_i in
  let t = Fixs.make_meta type_i in
  let env = Fixs.make_meta env_i in
  Axiom (judgement (cons e t env) e t)

(* `abst` inference rule *)
let rule_abst () =
  let x = meta_string () in
  let e = Fixs.make_meta expr_i in
  let abst_e = valu (abst x e) in
  let t1 = Fixs.make_meta type_i in
  let t2 = Fixs.make_meta type_i in
  let env = Fixs.make_meta env_i in
  let env' = cons (valu (var x)) t1 env in
  Infer (judgement env abst_e (arrow t1 t2),
         [Infer (judgement env' e t2, [])])
...
(* infer_rule_list : (unit -> rule_t) list *)
let infer_rule_list = [rule_vars; rule_abst; ... ]

Note that you should declare a list of all rules and it must be named `infer_rule_list`. Each element is the type of rule_t, which has two constructors:

• Axiom {top_i-th term}
• Infer {top_i-th term conclusion, list of premises}

Once you've finished to define the terms and rules, you can build them.

• Go to miki directory and execute `make bcl`
• Save your file as `user.ml`.
• Run `make` in your directory.
• Execute `js_of_ocaml {generated_binary_file_name}`, and it will generate a JS file.
• Open HTML file in your directory with your web browser.